Why the happy puppies? (as if happy puppies needed justification!)

Genuinely accessible to beginners:

• An entire chapter on Bayes' rule, with intuitive examples and emphasis on application to data and models.
• Preliminary chapters regarding concepts of probability, including probability density and conditional probabilities.
• Unique pedagogical treatment of Markov chain Monte Carlo (MCMC) methods.
• Unique pedagogical tutorial on hierarchical models.
• Richly illustrated.

Broad coverage of topics:

• Bayesian experiment design (power analysis and sample size planning).
• Bayesian model comparison (e.g., transdimensional MCMC).
• Bayesian ANOVA, including extensive treatment of multiple comparisons and interaction, using a hierarchical prior.
• Bayesian contingency table analysis (analogous to traditional chi-square tests).
• Bayesian multiple linear regression, with interaction terms.
• Bayesian logistic regression.
• Bayesian ordinal regression.
• Discussion and examples of repeated measures.
• Robust regression and ANOVA for outliers.
• Bayesian null hypothesis testing.
• See Chapter 1 and the Table of Contents.

Complete programs in R and BUGS and JAGS:

• Includes introduction to R and BUGS, which are freely available software packages.
• Dozens of complete analysis programs are included, with presentation graphics commands.

Extensive exercises:

• Every exercise has an explicitly stated purpose.
• Hints are provided for many exercises.
• Complete solutions are available to instructors (see below).

Look Inside: See samples below and more at Amazon.com and other online vendors.
Chapter 1	Table of Contents

Endorsements and Reviews:

"I think it fills a gaping hole in what is currently available, and will serve to create its own market as researchers and their students transition towards the routine application of Bayesian statistical methods."
Michael D. Lee, Professor, University of California, Irvine, and President of the Society for Mathematical Psychology.

"John Kruschke has written a book on statistics
It's better than others for reasons stylistic
It also is better because it is Bayesian
To find out why, buy it -- it's truly amazin'! "
James L. (Jay) McClelland, Lucie Stern Professor & Chair, Dept. of Psychology, Stanford University.

For several published reviews, see the blog.

About the author: John K. Kruschke has taught Bayesian data analysis, mathematical modeling, and traditional statistical methods for over 20 years. He is seven-time winner of Teaching Excellence Recognition Awards from Indiana University, where he is Professor of Psychological and Brain Sciences, and Adjunct Professor of Statistics. He has also presented numerous tutorials, workshops, or symposia on Bayesian data analysis (see this partial list). His research interests include the science of moral judgment, applications of Bayesian methods to adaptive teaching and learning, and models of attention in learning, which he has developed in both connectionist and Bayesian formalisms. He received a Troland Research Award from the National Academy of Sciences. He is an Action Editor for the Journal of Mathematical Psychology, and he is or has been on the editorial boards of several journals, including Psychological Review, the Journal of Experimental Psychology: General, and Psychonomic Bulletin & Review.

Why go Bayesian?

• An open letter explaining why it's time to go Bayesian.
• An article^* that explains a critical flaw of p-values in null hypothesis significance testing, and two different Bayesian approaches to assessing null values.
  Kruschke, J. K. (2010). Bayesian data analysis. Wiley Interdisciplinary Reviews: Cognitive Science, 1(5), 658-676. (doi:10.1002/wcs.72)
• An article^* that emphasizes advantages of Bayesian data analysis and the fact that Bayesian data analysis is appropriate regardless of the status of Bayesian models of cognition.
  Kruschke, J. K. (2010). What to believe: Bayesian methods for data analysis. Trends in Cognitive Sciences, 14(7), 293-300. (doi:10.1016/j.tics.2010.05.001)
• More at the blog!

Getting and using the book's computer programs:

Errata:

Discussion & FAQ & Blog:

See the latest discussion and suggest new topics at the blog!

• Why are there happy puppies on the cover? See this blog entry. If the puppies bother you, see a solution at this other blog entry.

• What editor is best for R programming? (in Windows) RStudio. See the blog entry for details, and runners up.

• ANOVA with non-homogeneous variances: An example where it matters. See the blog entry!

• Why does the book use highest density intervals (HDI's) instead of equal-tailed intervals? (Definition: The 95% equal-tailed interval excludes 2.5% of the distribution in each tail.) When a distribution is symmetric, equal-tailed and highest-density intervals are the same. When a distribution is skewed, however, equal-tailed intervals have an undesirable characteristic: Some of the points excluded in the compact tail have higher credibility than points included near the skewed tail. HDI's, however, are intuitively clear: Points inside the interval have higher credibility than points outside the interval. (Detractors of HDI's point out that they change under non-linear transformations of the parameter. Despite this fact, I still prefer HDI's because parameter scales usually have meaning for the modeler and aren't arbitrarily transformed. There is only one place in the textbook where a parameter is arbitrarily transformed merely to make the posterior less skewed for plotting purposes; see log(κ) in Figure 13.4, p. 351. The peril of making the transformation is not pointed out in the book because the conclusions are not affected in that example.)

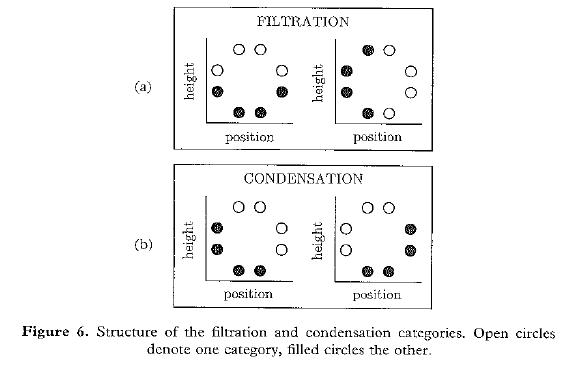• The filtration / condensation example on p. 220. See the figure at right (taken from Kruschke, 1993), which shows the specific combinations of height and line position that constitute a filtration structure and a condensation structure.

• More at the blog.

Solutions to exercises: